guglshoes.blogg.se - Matlab system of equations solver

#MATLAB SYSTEM OF EQUATIONS SOLVER HOW TO#
#MATLAB SYSTEM OF EQUATIONS SOLVER UPDATE#

This block is used to display the output of the program. Place this block at the output of the constraint block.From this section select the display block as shown in the figure below,.Now select the sinks section from the library browser of simulink as shown in the figure below, At the input of that block connect the output of the adder.From the math operations section select the Algebraic constraints block as shown in the figure below, The initial value provided to the constraint block is zero here. The output of the block must be provided to the input co-efficient through a feedback loop and with each iteration the output value will be updated until we receive a correct value for that unknown. This constraint block inputs a function whose input should be equal to zero and estimates the output of the functions value. The next step here is to place an Algebraic constraint block. This is the adder of equation 1 so we will name the gain and constant as a1, b1 and k1.two gain blocks and a constant with the help of a wire as shown in the figure below, At the input of the add block connect all the already placed blocks i.e.Double click on the add block, and in the list of signs add a + sign to increase the number of inputs as shown in the figure below,

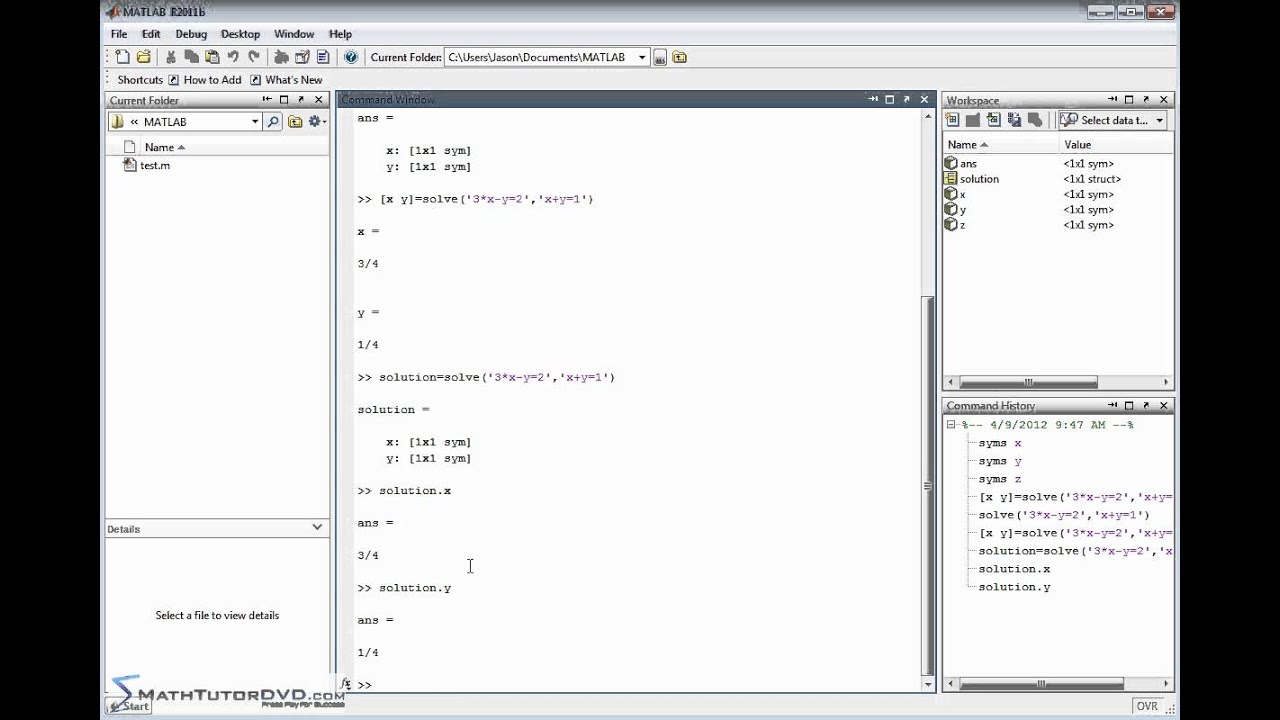
#MATLAB SYSTEM OF EQUATIONS SOLVER UPDATE#

As you can see the number of inputs provided by this add block is two, however, we want to add up three things together (two gain blocks and one constant) we thus now need to update the parameters of add block.

This add block will do the same job as the sum block we have used in previous tutorials.

From this section select the add block as shown in the figure below,.

From the library browser click on the Math operations section as shown in the figure below, To do so we can also use the sum block but as we are interested in exploring more blocks in simulink we will use another block provided by simulink to add up things together.

Now what we need to do is to add all these three blocks.

From the commonly used blocks section in the library browser of simulink, select the block of a constant and place it with the two already placed gain blocks as shown in the figure below, The constant at the right hand side of the equation can be placed in the block diagram in the form of a constant block. As we are using a system of equations with two unknowns hence the number of gain blocks is two.

These gain blocks are used to enter the value of the co-efficient of each of the variables, hence the number of gain blocks is equal to the number of unknowns in the equation.

Place two such gain blocks as the example we have taken here is for two unknown variables, as shown in the figure below, From that section select the gain block and drag and drop that gain block on the simulink block diagram section. After that open the library browser and from the library browser select the commonly used blocks as we have been doing in previous tutorials. Open MATLAB and then Simulink as we have done in previous tutorials. Lets’ now begin with the programming part. However, it is not that simple we also have to apply some logic in order to solve the system of linear equations. In Simulink a block named as Algebraic Constraint will help us do the job for us. Lets’ now move towards a simple example for solving the system of linear equations using Simulink.

#MATLAB SYSTEM OF EQUATIONS SOLVER HOW TO#

How to solve linear equations with Simulink These values will be used in the tutorial later. In this tutorial we are going to solve a system of linear equations with two equations and two unknowns and the equations are given below, For instance, if the system contains 5 linear equations then the number of unknown or variables in all these equations collectively is also 5 with each equation satisfying the definition of linear equations (having the power of each variable equal to 1). The number of equations is equal to the number of unknowns present in the equation. A system of linear equations is, however, a set of linear equations which contains same variable. The graph of a linear equation is a straight line. Where m is the slope of the line and c is the y-intercept. How to solve linear equations with Simulink Introduction to linear equation and system of linear equationsĪ linear equation is a mathematical term which is in the form of unknown variables whose power is one and which can be written in the form of point slope equation as given below,.Introduction to linear equation and system of linear equations.